Подглядывание в 🆎 тестах. Я ошибся, я могу один раз ошибиться?
Всем привет! В этом посте я хочу затронуть одну из базовых проблем, с которыми сталкивалось большинство людей - это проблема подглядывания.
В чем основная суть?
Предположим, мы запустили эксперимент, который должен идти 14 дней (так мы определили по дизайну). Возьмем для примера базовый t-test для двух выборок.
Вдруг мы решили посмотреть на результаты, видим значимое изменение. По сути (если мы знаем формулу для t-test'а или другого статистического критерия), накопительно на каждый день можем посчитать статистику и увидеть, что, например, в 4 день (ладно-ладно, в 7), мы увидели значимое изменение. Пришла в головугениальная мысль отрубить тест и экстраполировать выводы, но так, очевидно делать нельзя, и вот почему:
1. Мы рассчитывали сроки эксперимента в зависимости от трафика. Чем меньше пользователей, тем сильнее шум.
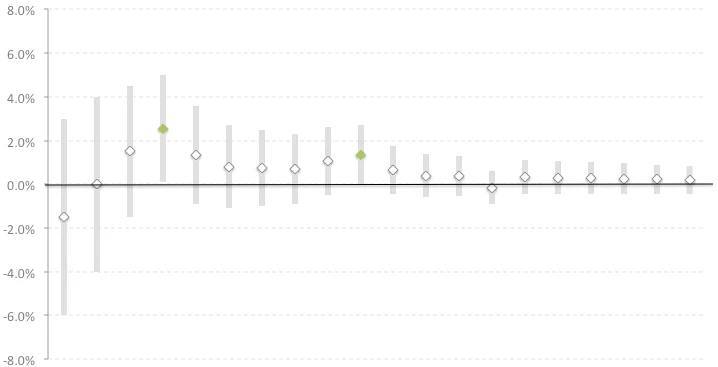
2. Доверительный интервал получается весьма широким, мы можем не до конца быть уверенными в эффекте (та же история может случиться и в обратную сторону, p-value от статистики (например, разницы средних) может "отскочить" от промежутка (0, alpha). Если бы мы подсмотрели, мы сделали неправильное решение.
3. На симуляциях мы повышаем ошибку первого рода (FPR) достаточно сильно. Подглядывание даже может имитировать подбрасывание монетки (по факту, мы проверяем несколько гипотез, что за 1, 2, 3, ... n день средние различаются, тем самым мы рискуем ошибиться. Подробнее можно посмотреть тут
Что можно посмотреть по этому поводу?
1. Статья от GoPractice..
2. Видео от Анатолия Карпова.
3. Пост от ProductSense на Facebook
Про это очень много есть статей + давно было интересно покопаться в проблеме подглядывания, например, ребята из Spotify использовали методы последовательного тестирования для досрочного принятия решения (чтобы не держать эксперимент какое-то время). История может быть актуальна, если мы хотим принимать правильные решения как можно чаще, а неправильные - сразу отрубать, чтобы не терять деньги во время теста. Также читал, что советуют обращаться к байесовскому тестированию, но давайте ко всему последовательно).
🐳 🐳 🐳 100 реакций на пост и разгоняем дальше 🐳 🐳 🐳
Всем привет! В этом посте я хочу затронуть одну из базовых проблем, с которыми сталкивалось большинство людей - это проблема подглядывания.
В чем основная суть?
Предположим, мы запустили эксперимент, который должен идти 14 дней (так мы определили по дизайну). Возьмем для примера базовый t-test для двух выборок.
Вдруг мы решили посмотреть на результаты, видим значимое изменение. По сути (если мы знаем формулу для t-test'а или другого статистического критерия), накопительно на каждый день можем посчитать статистику и увидеть, что, например, в 4 день (ладно-ладно, в 7), мы увидели значимое изменение. Пришла в голову
1. Мы рассчитывали сроки эксперимента в зависимости от трафика. Чем меньше пользователей, тем сильнее шум.
2. Доверительный интервал получается весьма широким, мы можем не до конца быть уверенными в эффекте (та же история может случиться и в обратную сторону, p-value от статистики (например, разницы средних) может "отскочить" от промежутка (0, alpha). Если бы мы подсмотрели, мы сделали неправильное решение.
3. На симуляциях мы повышаем ошибку первого рода (FPR) достаточно сильно. Подглядывание даже может имитировать подбрасывание монетки (по факту, мы проверяем несколько гипотез, что за 1, 2, 3, ... n день средние различаются, тем самым мы рискуем ошибиться. Подробнее можно посмотреть тут
Что можно посмотреть по этому поводу?
1. Статья от GoPractice..
2. Видео от Анатолия Карпова.
3. Пост от ProductSense на Facebook
Про это очень много есть статей + давно было интересно покопаться в проблеме подглядывания, например, ребята из Spotify использовали методы последовательного тестирования для досрочного принятия решения (чтобы не держать эксперимент какое-то время). История может быть актуальна, если мы хотим принимать правильные решения как можно чаще, а неправильные - сразу отрубать, чтобы не терять деньги во время теста. Также читал, что советуют обращаться к байесовскому тестированию, но давайте ко всему последовательно).