Возьмем какое-то количество одинаковых квадратов, скажем пять. Предположим, мы хотим упаковать их вместе внутри друого большого квадрата - насколько большим он обязан быть? Например, мы можем взять большой квадрат 3x3, в котором умещаются 9 маленьких квадратов. Пять наших поставить, а четыре остаются пустыми. Тогда у большого квадрата длина стороны выходит 3 (считая в размерах маленьких квадратиков).
Но оказывается, можно поставить четыре маленьких по углам близко друг к другу, но не касаясь, а пятый повернуть на 45 градусов и в середину между ними. Так они уложатся в большой квадрат с длиной стороны примерно 2.7, это лучше, чем 3. Возникает вопрос: насколько можно уменьшить большой квадрат, запаковав маленькие наиболее эффективно? И такой вопрос задается для каждого числа маленьких квадратов, необязательно пяти.
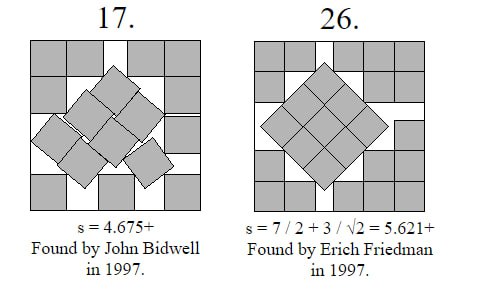
Математик Эрик Фридман исследует этот вопрос и опубликовал набор лучших известных результатов для разных n (n это число маленьких квадратов). Для некоторых написано "proved", это значит строго доказано, для других "found" - это лучшее, что найдено, но не доказано, что нельзя еще лучше. Мне очень нравится результат для n=17 своей хаотичностью и асимметрией. В Твиттере кто-то написал "бог умер и его убил лучший способ упаковать 17 квадратиков в большой квадрат".
Сравните его с красивой симметрией n=26.
Спросите себя: я человек-17 или человек-26?
Но оказывается, можно поставить четыре маленьких по углам близко друг к другу, но не касаясь, а пятый повернуть на 45 градусов и в середину между ними. Так они уложатся в большой квадрат с длиной стороны примерно 2.7, это лучше, чем 3. Возникает вопрос: насколько можно уменьшить большой квадрат, запаковав маленькие наиболее эффективно? И такой вопрос задается для каждого числа маленьких квадратов, необязательно пяти.
Математик Эрик Фридман исследует этот вопрос и опубликовал набор лучших известных результатов для разных n (n это число маленьких квадратов). Для некоторых написано "proved", это значит строго доказано, для других "found" - это лучшее, что найдено, но не доказано, что нельзя еще лучше. Мне очень нравится результат для n=17 своей хаотичностью и асимметрией. В Твиттере кто-то написал "бог умер и его убил лучший способ упаковать 17 квадратиков в большой квадрат".
Сравните его с красивой симметрией n=26.
Спросите себя: я человек-17 или человек-26?