🚀 @SBERLOGASCI webinar on mathematics:
👨🔬 А.Червов (к.ф.-м.н) "Базовые понятия теории представлений групп"
⌚️Пятница 7 июня 19.00 (по Москве)
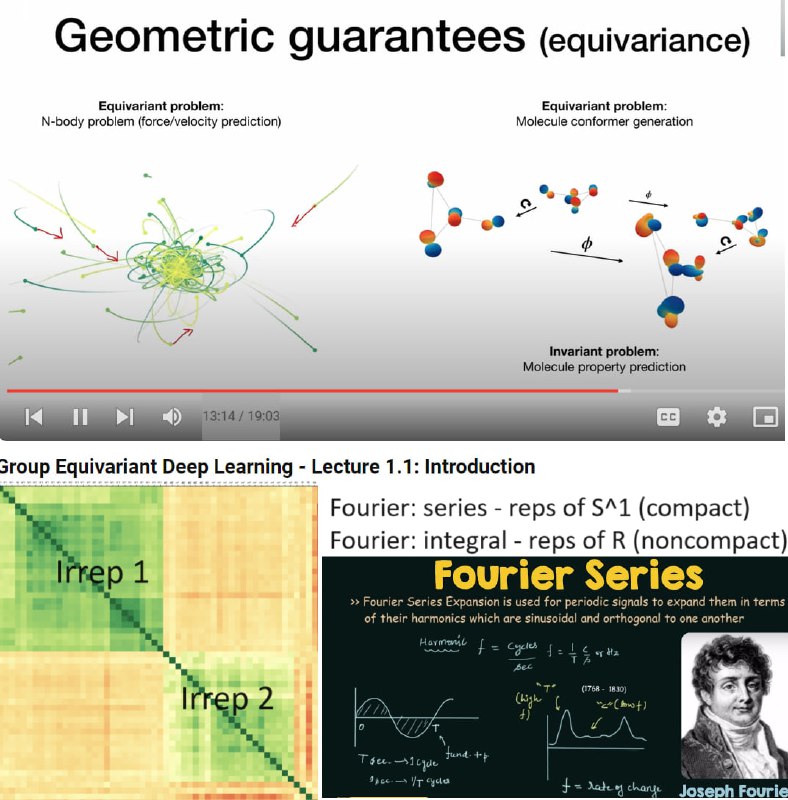
Последние годы в машинном обучении - стали появляться, так называемые, эквивариантные нейронные сети. (См. M.Welling: "Group equivariant convolutional networks", или лекции - https://www.youtube.com/playlist?list=PL8FnQMH2k7jzPrxqdYufoiYVHim8PyZWd ).
Для тех кто интересуется этой темой в данной лекции мы рассмотрим на пальцах основные понятия теории представлений групп.
Поясним следующие вещи - неприводимые представления (это блоки из которые все строится, разбиение на неприводимые - похоже на кластеризацию), операции с ними.
Полезно понимать - аналогии: если группа совсем простая - коммутативная - то теория представлений - это про ряды/интегралы Фурье. То есть для общих групп представления в некотором высшем смысле обобщают ряды Фурье.
С представлениями можно делать следующие - брать прямую сумму, и можно тензорно множить. Тензорное (кронекерово) произведение - можно думать так - функции от одной переменной тензорно умножить на себя - это рассмотреть функции от двух переменных.
Что такое группа - можно думать так - просто набор матриц, такой, что произведение матриц из набора лежит снова в наборе, обратная тоже в наборе ну единичная в нем. А смысл в этом какой ? Смысл - описывать разные симметрии - вращения, сдвиги и так далее.
Если есть две группы G,H можно рассмотреть их произведение GxH , как устроены представления GxH ? Ответ - V tensor W - тензорные произвдения представлений одной на другое.
Регулярное представление - то есть представления когда группа действует сама на себе. Важно понимать - что там живут вообще все представления - и как они там живут - каждое непривод. представление живет там в виде V tensor V^* (само на себя ну почти) - почему так ? ну потому что GxG действует на самом деле на G и см. пункт выше.
📹 Video: https://youtu.be/DQNQowfj_Ws?si=br0K_-2NDO4dglyK
📖 Presentation
👨🔬 А.Червов (к.ф.-м.н) "Базовые понятия теории представлений групп"
⌚️Пятница 7 июня 19.00 (по Москве)
Последние годы в машинном обучении - стали появляться, так называемые, эквивариантные нейронные сети. (См. M.Welling: "Group equivariant convolutional networks", или лекции - https://www.youtube.com/playlist?list=PL8FnQMH2k7jzPrxqdYufoiYVHim8PyZWd ).
Для тех кто интересуется этой темой в данной лекции мы рассмотрим на пальцах основные понятия теории представлений групп.
Поясним следующие вещи - неприводимые представления (это блоки из которые все строится, разбиение на неприводимые - похоже на кластеризацию), операции с ними.
Полезно понимать - аналогии: если группа совсем простая - коммутативная - то теория представлений - это про ряды/интегралы Фурье. То есть для общих групп представления в некотором высшем смысле обобщают ряды Фурье.
С представлениями можно делать следующие - брать прямую сумму, и можно тензорно множить. Тензорное (кронекерово) произведение - можно думать так - функции от одной переменной тензорно умножить на себя - это рассмотреть функции от двух переменных.
Что такое группа - можно думать так - просто набор матриц, такой, что произведение матриц из набора лежит снова в наборе, обратная тоже в наборе ну единичная в нем. А смысл в этом какой ? Смысл - описывать разные симметрии - вращения, сдвиги и так далее.
Если есть две группы G,H можно рассмотреть их произведение GxH , как устроены представления GxH ? Ответ - V tensor W - тензорные произвдения представлений одной на другое.
Регулярное представление - то есть представления когда группа действует сама на себе. Важно понимать - что там живут вообще все представления - и как они там живут - каждое непривод. представление живет там в виде V tensor V^* (само на себя ну почти) - почему так ? ну потому что GxG действует на самом деле на G и см. пункт выше.
📹 Video: https://youtu.be/DQNQowfj_Ws?si=br0K_-2NDO4dglyK
📖 Presentation