🚀 @SBERLOGASCI webinar on data science:
👨🔬 Александр Червов, Никита Бухал "Задача короткого пути на графе Кэли как задача перевода с "Пермутляндского" на "Кэлиляндский" - первый пример".
⌚️ 18 Апреля , Четверг, 19.00 по Москве
Задача нахождения пути на графах Кэли может быть переформулирована как задача секвенс-то-секвенс ("перевода" с одного "языка" на другой). Специфика графов Кэли - что любой путь на графе - задаётся как секвенс ребер/"мувов"/образующих группы ("Кэлиляндский"). С другой стороны любая вершина - просто перестановка чисел (1,2,3,...n) ("Пермутляндский"). Тем самым задача поиска пути из заданной перестановки в "стандартное/собранное" состояние - это задача перевода сиквенса длины "n" описывающего перестановку в сиквенс неизвестной длины описывающий последовательность "мувов" которые приводят заданную перестановку в "собранный"/стандартный вид (1,2,3,4,...).
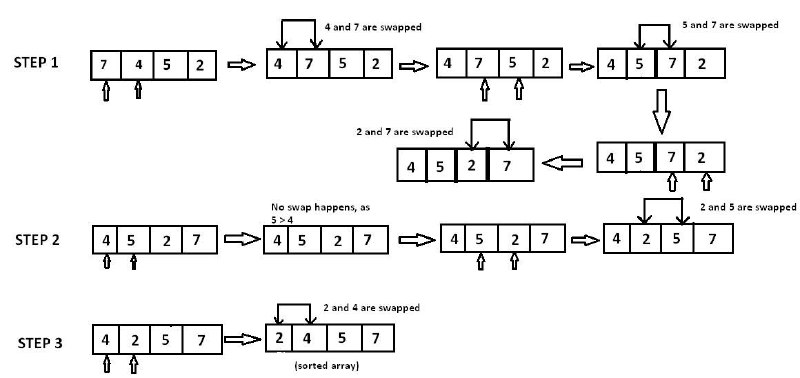
В данном докладе мы обсудим эти формулировки задач, а потом разберем первый пример - граф Кэли пермутохедрона , "мувы" = транспозиции соседей (i, i+1). То есть "сортировка пузырьком".
Решение на основе трансформера.
Исходная последовательность длинна N=8 s0 = [0, 1, 2, 3, 4, 5, 6, 7]
Tgt последовательность длинны N-1=7 [1, 2, 6, 0, 3, 4, 5]
Действуем последовательностью tgt на S0 так чтобы j = tgt[i] означает переставноку соседних элементов: s0[j] <-> s0[j+1].
В итоге получим последовательность src = tgt(s0) = [2, 0, 3, 4, 5, 7, 1, 6].
При этом tgt и tgt' считаются эквивалентными если tgt(s0) = tgt'(s0)
Задача: восстановить tgt из src
Алгоритм известен: записать в обратном порядке индексы соседних перестановок выполняя сориторвку пузырьеком:
0: [0, 2, 3, 4, 5, 7, 1, 6]
5: [0, 2, 3, 4, 5, 1, 7, 6]
6: [0, 2, 3, 4, 5, 1, 6, 7]
4: [0, 2, 3, 4, 1, 4, 6, 7]
3: [0, 2, 3, 1, 4, 4, 6, 7]
2: [0, 2, 1, 3, 4, 4, 6, 7]
1: [0, 1, 2, 3, 4, 4, 6, 7]
tgt' = [1, 2, 3, 4, 6, 5, 0] //<- То что хотим найти так как эквивалентна tgt [1, 2, 6, 0, 3, 4, 5]
Zoom link @sberlogabig before start. Videos: https://www.youtube.com/c/SciBerloga - subscribe !
👨🔬 Александр Червов, Никита Бухал "Задача короткого пути на графе Кэли как задача перевода с "Пермутляндского" на "Кэлиляндский" - первый пример".
⌚️ 18 Апреля , Четверг, 19.00 по Москве
Задача нахождения пути на графах Кэли может быть переформулирована как задача секвенс-то-секвенс ("перевода" с одного "языка" на другой). Специфика графов Кэли - что любой путь на графе - задаётся как секвенс ребер/"мувов"/образующих группы ("Кэлиляндский"). С другой стороны любая вершина - просто перестановка чисел (1,2,3,...n) ("Пермутляндский"). Тем самым задача поиска пути из заданной перестановки в "стандартное/собранное" состояние - это задача перевода сиквенса длины "n" описывающего перестановку в сиквенс неизвестной длины описывающий последовательность "мувов" которые приводят заданную перестановку в "собранный"/стандартный вид (1,2,3,4,...).
В данном докладе мы обсудим эти формулировки задач, а потом разберем первый пример - граф Кэли пермутохедрона , "мувы" = транспозиции соседей (i, i+1). То есть "сортировка пузырьком".
Решение на основе трансформера.
Исходная последовательность длинна N=8 s0 = [0, 1, 2, 3, 4, 5, 6, 7]
Tgt последовательность длинны N-1=7 [1, 2, 6, 0, 3, 4, 5]
Действуем последовательностью tgt на S0 так чтобы j = tgt[i] означает переставноку соседних элементов: s0[j] <-> s0[j+1].
В итоге получим последовательность src = tgt(s0) = [2, 0, 3, 4, 5, 7, 1, 6].
При этом tgt и tgt' считаются эквивалентными если tgt(s0) = tgt'(s0)
Задача: восстановить tgt из src
Алгоритм известен: записать в обратном порядке индексы соседних перестановок выполняя сориторвку пузырьеком:
0: [0, 2, 3, 4, 5, 7, 1, 6]
5: [0, 2, 3, 4, 5, 1, 7, 6]
6: [0, 2, 3, 4, 5, 1, 6, 7]
4: [0, 2, 3, 4, 1, 4, 6, 7]
3: [0, 2, 3, 1, 4, 4, 6, 7]
2: [0, 2, 1, 3, 4, 4, 6, 7]
1: [0, 1, 2, 3, 4, 4, 6, 7]
tgt' = [1, 2, 3, 4, 6, 5, 0] //<- То что хотим найти так как эквивалентна tgt [1, 2, 6, 0, 3, 4, 5]
Zoom link @sberlogabig before start. Videos: https://www.youtube.com/c/SciBerloga - subscribe !