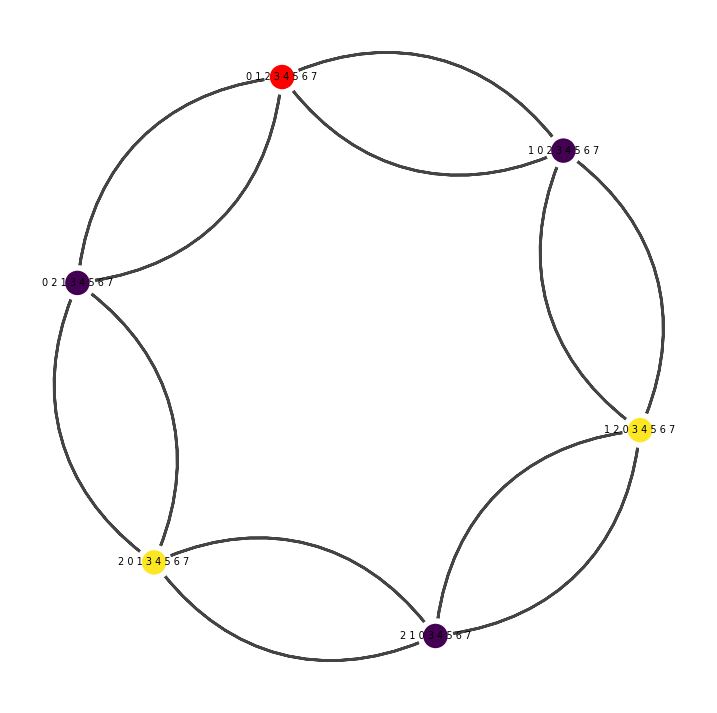
🚀 Что это за графы ? Это примеры графов Кэли для группы перестановок и стандартных образующих.
Напомним, что графы Кэли - краеугольной камень современной математики, и о них есть много нерешенных математических гипотез, которые мы надеемся продвинуть с помощью методов машинного обучения. Если Вам интересно присоединиться - отметьтесь в голосовалке : https://t.me/sberlogasci/7794
🚀 Графы Кэли/Шрейра определяются довольно просто - берем набор векторов (элементов группы/ее представления) и набор матриц (образующих группы). Вершины - вектора , ребро есть между x,y - если существует матрица из набора, что x = M y. И все ! Понятно - ребенку.
🚀 Владимир (автор замечательного канала @chelovek_nauk ) сделал ноутбук https://www.kaggle.com/code/shitovvladimir/visualization-of-cayley-graphs с визуализацией примеров этих графов. Апвоуты Каггл ноутбука - приветствуются , а также рекомендуем подписаться на его канал @chelovek_nauk!
🚀 Но при всей простоте, понимание свойств этих графов - например, оценка диаметра или гипотеза Ловаса о существовании гамильтонова пути - не поддаются усилиям лучших умов математики, включая Филсовдких медалистов Т. Тао, Т. Говерс, Ж. Бурген ... Но может быть именно Вы сможете решить эти проблема ? ) Присоединяйтесь - к нашей активности: https://t.me/sberlogasci/7794 .
Напомним, что графы Кэли - краеугольной камень современной математики, и о них есть много нерешенных математических гипотез, которые мы надеемся продвинуть с помощью методов машинного обучения. Если Вам интересно присоединиться - отметьтесь в голосовалке : https://t.me/sberlogasci/7794
🚀 Графы Кэли/Шрейра определяются довольно просто - берем набор векторов (элементов группы/ее представления) и набор матриц (образующих группы). Вершины - вектора , ребро есть между x,y - если существует матрица из набора, что x = M y. И все ! Понятно - ребенку.
🚀 Владимир (автор замечательного канала @chelovek_nauk ) сделал ноутбук https://www.kaggle.com/code/shitovvladimir/visualization-of-cayley-graphs с визуализацией примеров этих графов. Апвоуты Каггл ноутбука - приветствуются , а также рекомендуем подписаться на его канал @chelovek_nauk!
🚀 Но при всей простоте, понимание свойств этих графов - например, оценка диаметра или гипотеза Ловаса о существовании гамильтонова пути - не поддаются усилиям лучших умов математики, включая Филсовдких медалистов Т. Тао, Т. Говерс, Ж. Бурген ... Но может быть именно Вы сможете решить эти проблема ? ) Присоединяйтесь - к нашей активности: https://t.me/sberlogasci/7794 .