О том как нейросеть кубик Рубика собирает
(или случайные блуждания на графе в поисках кратчайшего пути)
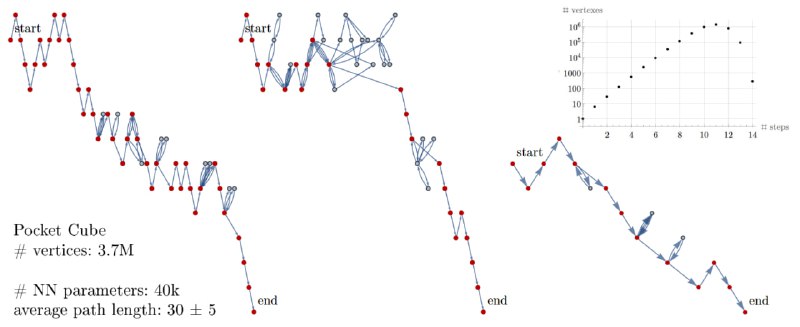
Возьмём кубик Рубика 2x2x2, от собранного состояния ■ делая всевозможные шаги найдём расстояние до всех состояний, таким образом получим граф с N=3.7М вершин степени 6. По пути мы нашли, что достаточно 14 шагов, чтобы дойти до ■ из любой позиции. Если блуждать случайно, то в среднем нужно будет сделать порядка N шагов, это явно не наш путь. Можно ли не запоминая все вершины научиться искать короткий путь до ■? Конечно да!
Например, возьмём 1М вершин и научим полносвязную трёхслойную нейронную сеть (40k параметров) понимать какое из рёбер уменьшает расстояние до ■. У меня модель даёт правильный ответ в 60% (на тестовых вершинах), чего уже оказывается достаточно! На графике приведены случайные блуждания в соответствие с предсказаниями модели. В среднем получается найти путь длиной 30 (если без поиска кратчайшего пути по посещенным вершинам, то 50), что по-моему замечательно)
(или случайные блуждания на графе в поисках кратчайшего пути)
Возьмём кубик Рубика 2x2x2, от собранного состояния ■ делая всевозможные шаги найдём расстояние до всех состояний, таким образом получим граф с N=3.7М вершин степени 6. По пути мы нашли, что достаточно 14 шагов, чтобы дойти до ■ из любой позиции. Если блуждать случайно, то в среднем нужно будет сделать порядка N шагов, это явно не наш путь. Можно ли не запоминая все вершины научиться искать короткий путь до ■? Конечно да!
Например, возьмём 1М вершин и научим полносвязную трёхслойную нейронную сеть (40k параметров) понимать какое из рёбер уменьшает расстояние до ■. У меня модель даёт правильный ответ в 60% (на тестовых вершинах), чего уже оказывается достаточно! На графике приведены случайные блуждания в соответствие с предсказаниями модели. В среднем получается найти путь длиной 30 (если без поиска кратчайшего пути по посещенным вершинам, то 50), что по-моему замечательно)