Корреляция и время
Фраза “Корреляция не означает причинно-следственную связь” стала уже максимально избитой. Но уже в который раз вижу, что эту фразу в контексте временных рядов понимают неверно. А с учеом того, что 90% табличных данных - по факту временные ряды (цены, продажи, фин показатели и тп) - неверно понимается почти всегда 😱
На каждом втором средненьком курсе по статистике вам расскажут пример ложной корреляции (те которая не означает причинно-следственную связь) между:
- потреблением мороженого и числом убийств
- обьемом потребления пищи и уровнем аутизма
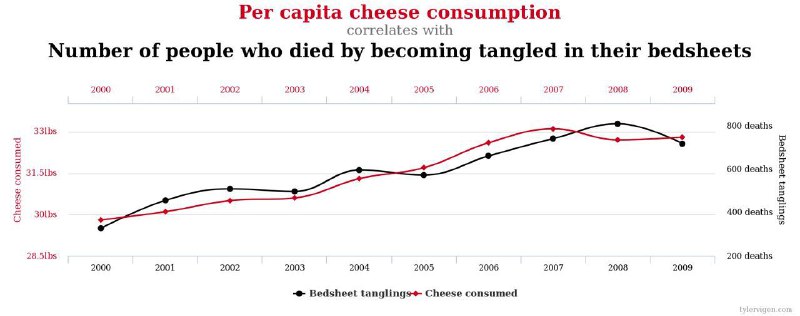
- потреблением сыра и смертностью от запутывания в одеяле кровати
Их все обьединяет то, что у двух показателей есть тренд во времени. И мы видим корреляцию на самом деле двух трендов, а не самих показателей
Проблема в том, что во временных рядах корреляцию и причинно-следственную связь ищут совсем не так:
*Упрощенно* алгоритм такой:
- Удалить трендовую и сезонную составляющую: e = y - trend - seasonal
- Если временной ряд не один, а много (1 показатель за 10 лет у разных стран, например), то нужно еще вычесть среднее значение каждой страны: e = y - trend - seasonal - group_mean
- После этого считать корреляцию остатков (e) у 2-ух переменных
Тогда никакой ложной корреляции, как в примерах выше, вы не увидите 👌
Ну и в целом, когда ничинаете работать с временными рядами, то очень много из классической статистики работает совсем не так: корреляция, стат значимоть коэффициентов регрессии, what-if анализ на изменение 1 фичи и тп. Тк что будьте крайне аккуратны: ведь временные ряды есть везде 😈
P.S. Хороший пример ложной корреляции - это когда есть 2 переменные, измеренные в 1 момент времени
Например, если вы за 1 день измерите размер стопы и длину волос у 10_000 людей, то найдете отрицательную значимую, но ложную корреляцию между этими показателями
Фраза “Корреляция не означает причинно-следственную связь” стала уже максимально избитой. Но уже в который раз вижу, что эту фразу в контексте временных рядов понимают неверно. А с учеом того, что 90% табличных данных - по факту временные ряды (цены, продажи, фин показатели и тп) - неверно понимается почти всегда 😱
На каждом втором средненьком курсе по статистике вам расскажут пример ложной корреляции (те которая не означает причинно-следственную связь) между:
- потреблением мороженого и числом убийств
- обьемом потребления пищи и уровнем аутизма
- потреблением сыра и смертностью от запутывания в одеяле кровати
Их все обьединяет то, что у двух показателей есть тренд во времени. И мы видим корреляцию на самом деле двух трендов, а не самих показателей
Проблема в том, что во временных рядах корреляцию и причинно-следственную связь ищут совсем не так:
*Упрощенно* алгоритм такой:
- Удалить трендовую и сезонную составляющую: e = y - trend - seasonal
- Если временной ряд не один, а много (1 показатель за 10 лет у разных стран, например), то нужно еще вычесть среднее значение каждой страны: e = y - trend - seasonal - group_mean
- После этого считать корреляцию остатков (e) у 2-ух переменных
Тогда никакой ложной корреляции, как в примерах выше, вы не увидите 👌
Ну и в целом, когда ничинаете работать с временными рядами, то очень много из классической статистики работает совсем не так: корреляция, стат значимоть коэффициентов регрессии, what-if анализ на изменение 1 фичи и тп. Тк что будьте крайне аккуратны: ведь временные ряды есть везде 😈
P.S. Хороший пример ложной корреляции - это когда есть 2 переменные, измеренные в 1 момент времени
Например, если вы за 1 день измерите размер стопы и длину волос у 10_000 людей, то найдете отрицательную значимую, но ложную корреляцию между этими показателями