Верный ответ на опрос выше - 3ий и 4ый
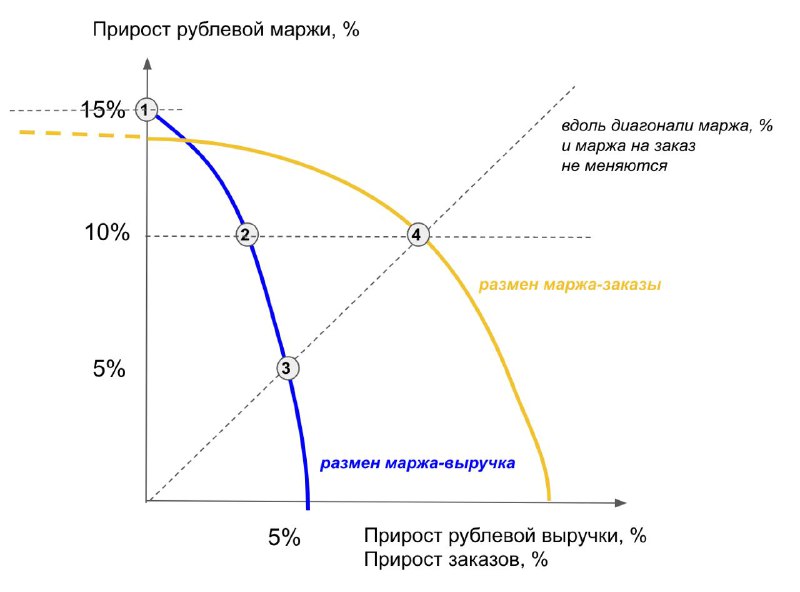
1) Точка 1 - а, б
В ней маржа +15%, выручка +0%
поэтому это точка максимума как маржи в руб, так и маржи в %
(!) Прелесть в том, что это кажется идеальным вариантом, но график вам немножко привирает 😈
Надо посмотреть на то, какой будет прирост заказов в этой точке. А он будет сильно отрицательным (пересечение продолжения оранжевой кривой и горизонтали от точки 3 где-то в отрицательной области оси Х)!
Возможно вы вырастите маржу на 15%, но снизите заказы условно в 2 раза (~потеряете кучу клиентов)
2) Точка 3 - в
Изменение маржи, % = маржа * (1 + delta_margin) / (выручка *(1 + delta_revenue)) = (маржа / выручка) * (1 + delta_margin) / (1 + delta_revenue)
чтобы маржа в % не менялось надо имет delta_margin = delta_revenue (как раз верно на диагонали)
Максимизация выручки - движение вправо вдоль оси Х. Максимальный сдвиг вправо, но не ниже диагонали дает нам точку
3 - в: максимум выручки при ограничении, что маржа в % не падает
3) Точка 2 - г
Вот тут интереснее
Ограничение, что маржа в руб не падает соответствует пересечению диагонали и оранжевой кривой (точка 4)
Чтобы его сохранить, но мыслить в размене маржа-выручка, нужно провести огранчение по горизонтали - мы не можем падать ниже горизонтали, двигаясь по синей кривой - это нам дает точку 2
Обратите внимание, и в точке 2, и в точке 3 мы максимизируем выручку при огрничении на маржинальность. Но оказывается, маржинальность = маржа / заказ накладывает сильно более жесткое ограничение (получаем прирост маржи в руб около 5% вместо 10%), чем маржа = маржа / выручка
1) Точка 1 - а, б
В ней маржа +15%, выручка +0%
поэтому это точка максимума как маржи в руб, так и маржи в %
(!) Прелесть в том, что это кажется идеальным вариантом, но график вам немножко привирает 😈
Надо посмотреть на то, какой будет прирост заказов в этой точке. А он будет сильно отрицательным (пересечение продолжения оранжевой кривой и горизонтали от точки 3 где-то в отрицательной области оси Х)!
Возможно вы вырастите маржу на 15%, но снизите заказы условно в 2 раза (~потеряете кучу клиентов)
2) Точка 3 - в
Изменение маржи, % = маржа * (1 + delta_margin) / (выручка *(1 + delta_revenue)) = (маржа / выручка) * (1 + delta_margin) / (1 + delta_revenue)
чтобы маржа в % не менялось надо имет delta_margin = delta_revenue (как раз верно на диагонали)
Максимизация выручки - движение вправо вдоль оси Х. Максимальный сдвиг вправо, но не ниже диагонали дает нам точку
3 - в: максимум выручки при ограничении, что маржа в % не падает
3) Точка 2 - г
Вот тут интереснее
Ограничение, что маржа в руб не падает соответствует пересечению диагонали и оранжевой кривой (точка 4)
Чтобы его сохранить, но мыслить в размене маржа-выручка, нужно провести огранчение по горизонтали - мы не можем падать ниже горизонтали, двигаясь по синей кривой - это нам дает точку 2
Обратите внимание, и в точке 2, и в точке 3 мы максимизируем выручку при огрничении на маржинальность. Но оказывается, маржинальность = маржа / заказ накладывает сильно более жесткое ограничение (получаем прирост маржи в руб около 5% вместо 10%), чем маржа = маржа / выручка