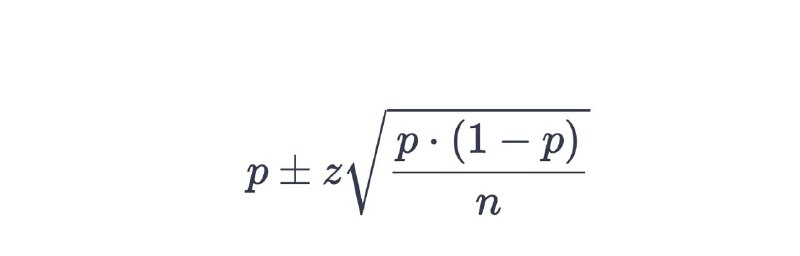
Вы баллотируетесь на пост, и ваш социолог опросил 100 избирателей, 60 из которых сказали, что собираются голосовать за вас. Можете ли вы быть уверены в победе?
Ответ
Примем для простоты, что у вас только один соперник.
Также примем, что желаемый доверительный интервал составляет 95%. Это даст нам z-оценку 1.96. Формула на картинке.
В нашей задаче p = 0.6, z = 1.96, n = 100, что дает доверительный интервал [50.4, 69.6].
Таким образом, при доверительном интервале 95% вы можете расслабиться, только если ничего не имеете против победы с минимальным перевесом. В противном случае придется добиться 61 голоса из 100 опрошенных, чтобы не беспокоиться.
@machinelearning_interview
Ответ
Примем для простоты, что у вас только один соперник.
Также примем, что желаемый доверительный интервал составляет 95%. Это даст нам z-оценку 1.96. Формула на картинке.
В нашей задаче p = 0.6, z = 1.96, n = 100, что дает доверительный интервал [50.4, 69.6].
Таким образом, при доверительном интервале 95% вы можете расслабиться, только если ничего не имеете против победы с минимальным перевесом. В противном случае придется добиться 61 голоса из 100 опрошенных, чтобы не беспокоиться.
@machinelearning_interview