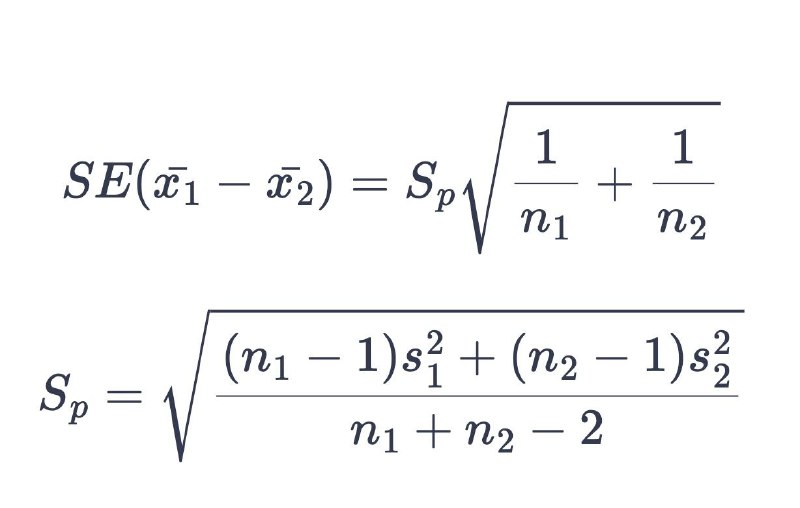
Для тестирования новой и старой систем сортировки пациентов неотложной помощи исследователи выбрали 20 ночей и случайным образом назначили новую систему сортировки на 10 из них, в остальных оставив старую. Они рассчитали среднее время ожидания (СВО) доктора для каждой ночи. Для новой системы СВО = 3 часа с отклонением 0.60, тогда как для старой было 5 часов с отклонением 0.68. Оцените 95% доверительный интервал для разницы в среднем СВО между системами. Считайте дисперсию постоянной.
Воспользуемся формулой нахождения доверительного интервала для двух независимых выборок (используем t-таблицу для n1+n2-2 степеней свободы)
Доверительный интервал – это среднее +/- t-оценка * стандартную ошибку.
Среднее значение = новое среднее – старое среднее = 3-5 = -2.
t-оценка равна 2.101, учитывая 18 степеней свободы (20-2) и 95% доверительный интервал (смотри Картинку).
Стандартная ошибка = sqrt(0.62*9+0.682*9)/(10+10–2)) * sqrt(1/10+1/10) = 0.352. Доверительный интервал = [-2.75, -1.25].
@machinelearning_interview
Воспользуемся формулой нахождения доверительного интервала для двух независимых выборок (используем t-таблицу для n1+n2-2 степеней свободы)
Доверительный интервал – это среднее +/- t-оценка * стандартную ошибку.
Среднее значение = новое среднее – старое среднее = 3-5 = -2.
t-оценка равна 2.101, учитывая 18 степеней свободы (20-2) и 95% доверительный интервал (смотри Картинку).
Стандартная ошибка = sqrt(0.62*9+0.682*9)/(10+10–2)) * sqrt(1/10+1/10) = 0.352. Доверительный интервал = [-2.75, -1.25].
@machinelearning_interview