Стало стыдно, что скинул статью без пояснений, почему она классная – исправлюсь.
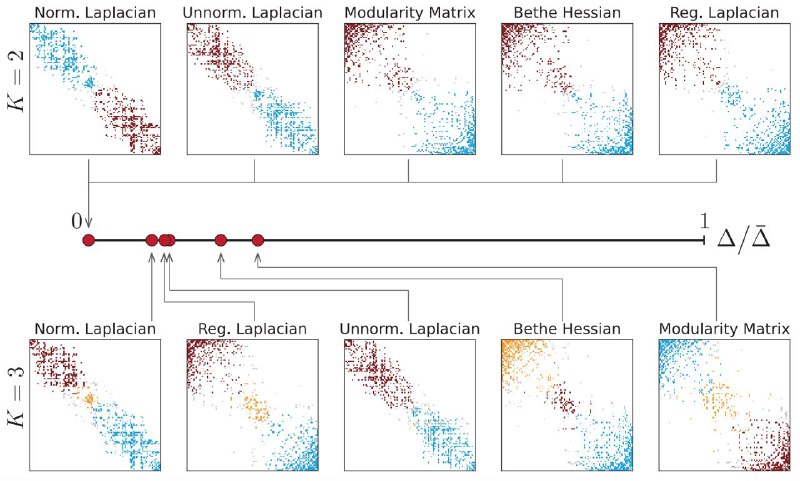
Задача о минимальном линейном расположении графа (minimum linear arrangement) – это такая дедовская задача о том, как расположить элементы в матрицы смежности таким образом, чтобы привести матрицу смежности к блочно-диагональному виду.
В первой же статье про эту проблему доказали, что она NP-полная, но рисёрчеры не успокаиваются, потому что проблема важная – чем лучше расположение, тем ближе в кэше наши рёбра, тем быстрее можно решать любые задачи.
Мне статья понравилась небольшим разбором разных не очень популярных матриц, использующихся для спектральной кластеризации, в контексте линейного расположения. Становится чуть понятнее, что делают параметры в матрицах типа регуляризованного Лапласиана и гессиана Бете.
Кстати, первый автор на днях психанул и основал стартап по созданию и анализу опросов. На основе кластеризации и упорядочивания графов, естестенно.💁♂️
Задача о минимальном линейном расположении графа (minimum linear arrangement) – это такая дедовская задача о том, как расположить элементы в матрицы смежности таким образом, чтобы привести матрицу смежности к блочно-диагональному виду.
В первой же статье про эту проблему доказали, что она NP-полная, но рисёрчеры не успокаиваются, потому что проблема важная – чем лучше расположение, тем ближе в кэше наши рёбра, тем быстрее можно решать любые задачи.
Мне статья понравилась небольшим разбором разных не очень популярных матриц, использующихся для спектральной кластеризации, в контексте линейного расположения. Становится чуть понятнее, что делают параметры в матрицах типа регуляризованного Лапласиана и гессиана Бете.
Кстати, первый автор на днях психанул и основал стартап по созданию и анализу опросов. На основе кластеризации и упорядочивания графов, естестенно.