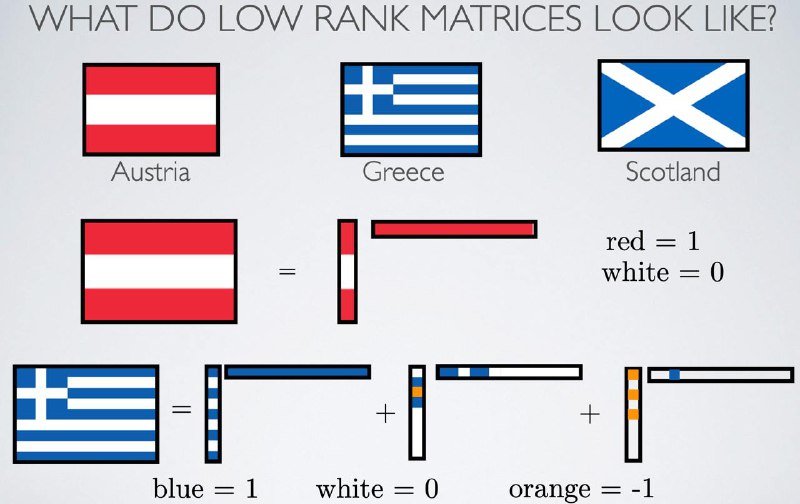
Почему почти у всех полезных матриц маленький ранг?
В нашей с вами жизни матрицы малого ранга встречаются на каждом шагу, например, в моделировании физических свойств физических систем (анализ теплопроводности или модальный анализ вибраций), в рекомендательных системах, сжатие изображений – везде, если поискать , можно найти матрицы с небольшим рангом.🧐
Это невероятно удобно: с матрицами малого ранга можно делать абсолютно неприличные вещи – например, для матрицы n × n ранга d можно восстановить все её элементы из случайно выбрав C*n^{1.2}*r*log n значений. Понятное дело, все операции – матвеки, подсчёт нормы и всяких разложений тоже существенно ускоряются. В наших любимых LLMках матрицы малого ранга используются для тюнинга и создания адаптеров для решения разнообразных задач.
При этом, случайные Гауссовские матрицы имеют (с огромной вероятностью) полный ранг. Каким-то образом получается, что для матриц "из жизни" ранг оказывается небольшим.🤪
Самое, наверное, известное – наш мир образуют гладкие функции (скалярные и векторные), а они порождают матрицы маленького ранга. На днях я набрёл на альтернативное объяснение (откуда украл картинку для поста): матрицы в реальном мире похожи на результат матричных уравнений Сильвестра. У таких матриц будет маленький displacement rank – он свойственен системам, где можно выбрать разные точки отсчёта. Оценки у ребят получаются довольно некрасивые (кому нравится считать числа Золотарёва?), но зато точные. Кстати, в этом нашем диплёрнинге low displacement rank matrices уже успели поприменять. Широко известные в узких кругах Albert Gu и Tri Dao тоже отметились.
Всем подписчикам желаем низкого ранга по жизни – ну, чтобы гладко всё было, да.👍
В нашей с вами жизни матрицы малого ранга встречаются на каждом шагу, например, в моделировании физических свойств физических систем (анализ теплопроводности или модальный анализ вибраций), в рекомендательных системах, сжатие изображений – везде, если поискать , можно найти матрицы с небольшим рангом.
Это невероятно удобно: с матрицами малого ранга можно делать абсолютно неприличные вещи – например, для матрицы n × n ранга d можно восстановить все её элементы из случайно выбрав C*n^{1.2}*r*log n значений. Понятное дело, все операции – матвеки, подсчёт нормы и всяких разложений тоже существенно ускоряются. В наших любимых LLMках матрицы малого ранга используются для тюнинга и создания адаптеров для решения разнообразных задач.
При этом, случайные Гауссовские матрицы имеют (с огромной вероятностью) полный ранг. Каким-то образом получается, что для матриц "из жизни" ранг оказывается небольшим.
Самое, наверное, известное – наш мир образуют гладкие функции (скалярные и векторные), а они порождают матрицы маленького ранга. На днях я набрёл на альтернативное объяснение (откуда украл картинку для поста): матрицы в реальном мире похожи на результат матричных уравнений Сильвестра. У таких матриц будет маленький displacement rank – он свойственен системам, где можно выбрать разные точки отсчёта. Оценки у ребят получаются довольно некрасивые (кому нравится считать числа Золотарёва?), но зато точные. Кстати, в этом нашем диплёрнинге low displacement rank matrices уже успели поприменять. Широко известные в узких кругах Albert Gu и Tri Dao тоже отметились.
Всем подписчикам желаем низкого ранга по жизни – ну, чтобы гладко всё было, да.