Не все доверительным интервалы одинаково полезны
Возвращаемся к техническим постам посленаучных каникул напряжённой летней работы. 🏄♂️
Доверительные интервалы для биномиального распределения – очень полезная в быту штука. Например, они всплывают, когда мы хотим "правильно" отранжировать товары по среднему отзыву – если взять среднее значение, сверху будут вещи с одним положительным отзывом. Некоторые сайты до сих пор этим грешат – амазон, например😑 . Вместо этого стоит использовать нижнюю границу доверительного интервала, и ранжирование станет намного лучше.
Один из самых известных тестов для этого – тест Вальда. Он до сих пор рекомендуется для биномиальных респределений во многих учебниках, например, в известном Casella & Berger. Однако, именно для биномиальных пропорций тест Вальда – очень плохая идея.📉
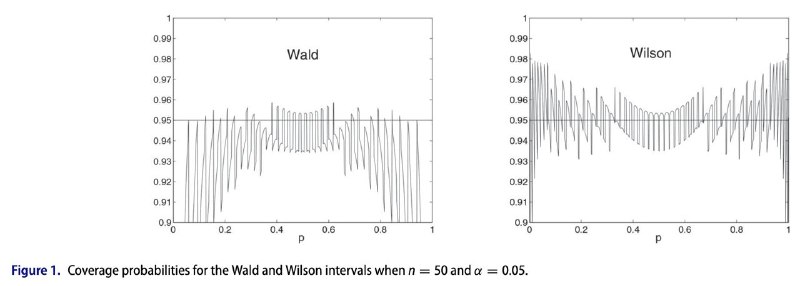
В других учебниках часто пишут про потерю силы на маленьких выборках, но основная проблема теста в том, что он теряет силу с приближением параметра p к 0 или 1 из-за эффекта Hauck–Donner, что можно увидеть на иллюстрации к посту. Про этот эффект есть несколько статей, ну или можно почитать более простую, которая недавно вышла в Teacher's Corner журнала The American Statistician. Там призывают перестать использовать тест Уилсона. Формула там подлиннее, зато нет проблем с покрытием.🍳
Кстати, интересно, что у других тестов вроде Agresti–Coull и Clopper–Pearson покрытие слишком консервативное (для Clopper–Peason это неудивительно, потому что покрытие там строго больше 1-α). Вот тут есть сравнение покрытия этих тестов с кодом на R (🤮 ).
Возвращаемся к техническим постам после
Доверительные интервалы для биномиального распределения – очень полезная в быту штука. Например, они всплывают, когда мы хотим "правильно" отранжировать товары по среднему отзыву – если взять среднее значение, сверху будут вещи с одним положительным отзывом. Некоторые сайты до сих пор этим грешат – амазон, например
Один из самых известных тестов для этого – тест Вальда. Он до сих пор рекомендуется для биномиальных респределений во многих учебниках, например, в известном Casella & Berger. Однако, именно для биномиальных пропорций тест Вальда – очень плохая идея.
В других учебниках часто пишут про потерю силы на маленьких выборках, но основная проблема теста в том, что он теряет силу с приближением параметра p к 0 или 1 из-за эффекта Hauck–Donner, что можно увидеть на иллюстрации к посту. Про этот эффект есть несколько статей, ну или можно почитать более простую, которая недавно вышла в Teacher's Corner журнала The American Statistician. Там призывают перестать использовать тест Уилсона. Формула там подлиннее, зато нет проблем с покрытием.
Кстати, интересно, что у других тестов вроде Agresti–Coull и Clopper–Pearson покрытие слишком консервативное (для Clopper–Peason это неудивительно, потому что покрытие там строго больше 1-α). Вот тут есть сравнение покрытия этих тестов с кодом на R (