Библиотека собеса по Data Science | вопросы с собеседований

Напишите код, который будет иллюстрировать Закон больших чисел (ЗБЧ)



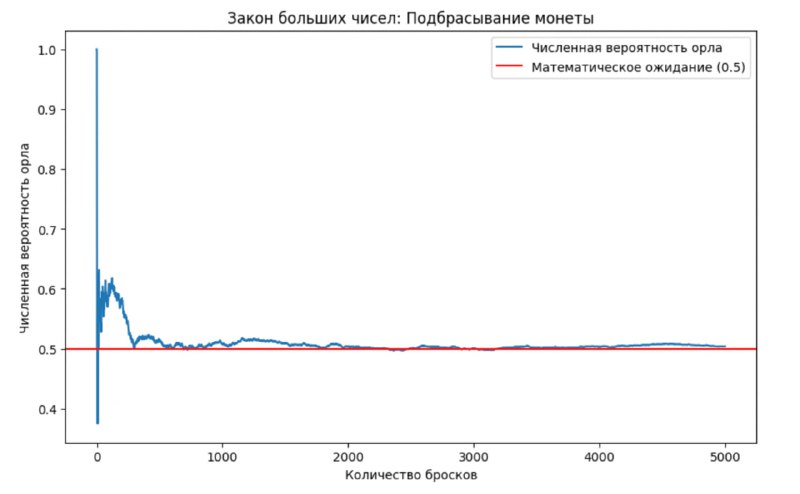
ЗБЧ утверждает, что при увеличении количества попыток случайная величина стремится к своему математическому ожиданию. Для иллюстрации возьмём подбрасывание честной монетки. Математическое ожидание выпадения орла равно 0.5. С увеличением числа подбрасываний среднее значение количества выпавших орлов должно приближаться к 0.5.

import random

import matplotlib.pyplot as plt



total_flips = 0

numerical_probability = []

H_count = 0



for i in range(0, 5000):

    new_flip = random.choice(['H', 'T'])  

    total_flips += 1

    if new_flip == 'H':

        H_count += 1

    numerical_probability.append(H_count / total_flips)  



plt.figure(figsize=(10, 6))

plt.plot(numerical_probability, label='Численная вероятность орла')

plt.axhline(y=0.5, color='r', linestyle='-', label='Математическое ожидание (0.5)')

plt.xlabel("Количество бросков")

plt.ylabel("Численная вероятность орла")

plt.title("Закон больших чисел: Подбрасывание монеты")

plt.legend()



plt.show()

#программирование

#теория_вероятностей